
Financial equity represents the ownership interest in a company’s assets after deducting liabilities. It reflects the value that belongs to the shareholders or owners of the business. https://www.bookstime.com/ Equity can also refer to other items like brand equity or other non-financial concepts. As part of its 2023 annual report, Apple reported $73.812 billion of shareholder equity.
Look at the balance sheet’s stockholders’ equity section
Get instant access to lessons taught by experienced private equity pros and bulge bracket investment bankers including financial statement modeling, DCF, M&A, LBO, Comps and Excel Modeling. Shareholder equity is not a perfect predictor of a company’s financial health. However, when used in conjunction with other tools and metrics, the investor can accurately assess an organization’s health. As a result, from an investor’s perspective, debt is the least risky investment.
- As far as limitations go, there are a few, starting with the fact that certain assets may not show up on a balance sheet.
- This is the other formula, where share capital, retained earnings, and treasury stock are needed to formulate owner’s equity.
- However, when used in conjunction with other tools and metrics, the investor can accurately assess an organization’s health.
- Retained earnings are part of shareholder equity as is any capital invested in the company.
- Stockholders’ equity refers to the assets of a company that remain available to shareholders after all liabilities have been paid.
Example of Shareholders’ Equity Calculation
During a liquidation process, the value of physical assets is reduced and there are other extraordinary conditions that make the two numbers incompatible. Retained earnings should not be confused with cash or other liquid assets. The retained earnings are used primarily for the expenses of doing business and for the expansion of the business. This is the percentage of net earnings that is not paid to shareholders as dividends. Long-term liabilities are obligations that are due for repayment over periods longer than one year. Companies may have bonds payable, leases, and pension obligations under this category.

Do you already work with a financial advisor?
It will show the total stockholders’ equity for the period, including its constituent parts, like common stock, preferred stock, and so on. The fundamental accounting equation is assets equalling the sum of liabilities and equity. This equation is the basis for the balance sheet, which summarizes a company’s financial position at a specific point in time. In all of the examples we’ve discussed in this article, the basis of calculating that equity was rooted in this accounting equation. To determine total assets for this equity formula, you need to add long-term assets as well as the current assets. In terms of payment and liquidation order, bondholders are ahead of preferred shareholders, who in turn are ahead of common shareholders.
In this formula, the equity of the shareholders is the difference between the total assets and the total liabilities. For example, if a company has $80,000 in total assets and $40,000 in liabilities, the shareholders’ equity is $40,000. Share capital is the sum of funds invested in a firm by its owners, represented by common and/or preference shares. Share capital differs from shareholder equity in that it represents the funds raised by issuing shares, while shareholder equity includes both share capital and retained earnings.
- Understanding stockholders’ equity and how it’s calculated can help you to make more informed decisions as an investor.
- The total stockholders’ equity for a given period represents the total at the end of the period.
- Shareholders’ equity can also be calculated by taking the company’s total assets less the total liabilities.
- Bonds are contractual liabilities where annual payments are guaranteed unless the issuer defaults, while dividend payments from owning shares are discretionary and not fixed.
- Stockholders’ equity measures the ratio of assets to liabilities in a company.
- So, you may want to check if Tidewater is trading on a high P/E or a low P/E, relative to its industry.
Some call this value « brand equity, » which measures the value of a brand relative to a generic or store-brand version of a product. Retained earnings, also known as accumulated profits, represents the cumulative business earnings minus dividends distributed to shareholders. However, the effect of dividends varies based on the type of dividends issued. Stock dividends have a different impact on shareholder equity than cash payments. No, when a corporation distributes cash dividends to its shareholders, the total sum of all dividends received is deducted from stockholders’ equity. A higher equity ratio indicates that shareholders’ equity finances a larger proportion of a company’s assets compared to other sources of financing.
How to Figure Out Beginning Stockholders’ Equity
- For example, many soft-drink lovers will reach for a Coke before buying a store-brand cola because they prefer the taste or are more familiar with the flavor.
- Shareholders, however, are concerned with both liabilities and equity accounts because stockholders equity can only be paid after bondholders have been paid.
- Created by the American chemicals corporation DuPont in the 1920s, this analysis reveals which factors are contributing the most (or the least) to a firm’s ROE.
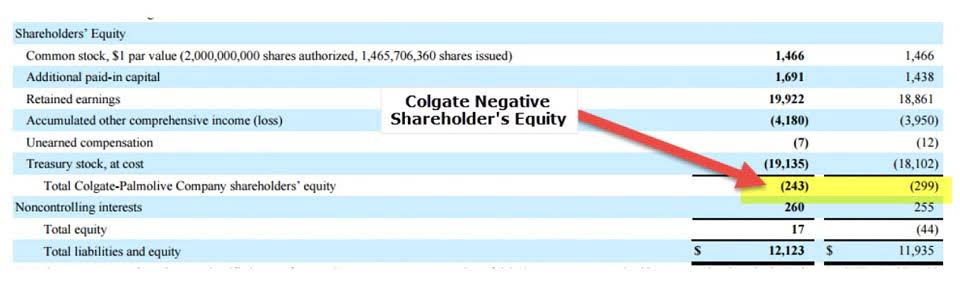
- As of September 30, 2023 (the date listed on the company’s 2023 annual report), the company had an accumulated deficit of $214 million.
- Sustainable growth rates and dividend growth rates can be estimated using ROE, assuming that the ratio is roughly in line or just above its peer group average.
- It informs business owners about when and how much money to spend and helps them make financial decisions.
- It comprises contributions by owners plus the accumulation of income produced by the firm and reinvested since its inception.
Next, the “Retained Earnings” are the accumulated net profits (i.e. the “bottom line”) that the company holds onto as opposed to paying dividends to shareholders. Otherwise, an alternative approach to calculating shareholders’ equity is to add up the following line items, which we’ll explain in more detail soon. Under a hypothetical liquidation scenario in which all liabilities are cleared off its books, how to calculate stockholders equity the residual value that remains reflects the concept of shareholders equity. A low level of debt means that shareholders are more likely to receive some repayment during a liquidation. However, there have been many cases in which the assets were exhausted before shareholders got a penny. Other creditors, including suppliers, bondholders, and preferred shareholders, are repaid before common shareholders.
How to Calculate Stockholders’ Equity
For example, utilities have many assets and debt on the balance sheet compared to a relatively small amount of net income. A technology or retail firm with smaller balance sheet accounts relative to net income may have normal ROE levels of 18% or more. Because net income is earned over a period of time and shareholders’ equity is a balance sheet account often reporting on a single specific period, an analyst should take an average equity balance. This is often done by taking the average between the beginning balance and ending balance of equity. Shareholders’ equity is, therefore, essentially the net worth of a corporation. If the company were to liquidate, shareholders’ equity is the amount of money that would theoretically be received by its shareholders.
Negative stockholders’ equity in that situation may be further compounded by negative cash flow. At a glance, stockholders’ equity can give you an idea of how well a company is doing financially and how likely it is to be able to pay its debts. That, in turn, can help you to decide if a company is worth investing in, based on your goals and risk tolerance. These earnings, reported as part of the income statement, accumulate and grow larger over time. At some point, accumulated retained earnings may exceed the amount of contributed equity capital and can eventually grow to be the main source of stockholders’ equity.
